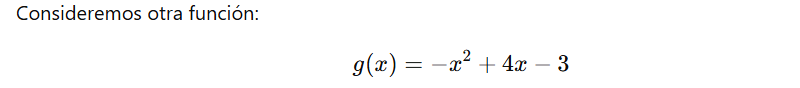Análisis de la segunda derivada
Las derivadas son una herramienta fundamental en el cálculo, con aplicaciones en muchas áreas, desde la física hasta la economía. La primera derivada de una función nos ayuda a entender el comportamiento de una curva, específicamente si la función está aumentando o disminuyendo en cierto intervalo. Sin embargo, la segunda derivada va un paso más allá: nos permite analizar la "forma" de la función. Al calcular la segunda derivada, podemos determinar si una función es cóncava o convexa, lo cual es clave para entender puntos de inflexión y maximizar o minimizar valores en problemas aplicados.
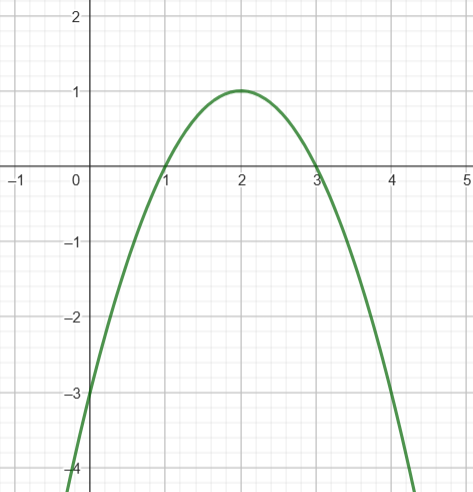
Una función es convexa hacia arriba cuando la curva de la función es como una "sonrisa" (forma de U), mientras que es cóncava hacia abajo cuando la curva parece una "mueca" (forma de ∩). La segunda derivada nos ayuda a identificar estos comportamientos, pues una función será convexa hacia arriba si su segunda derivada es positiva en un intervalo, y cóncava hacia abajo si la segunda derivada es negativa en el mismo. A continuación, veremos dos ejemplos que ilustran cómo se determina la concavidad con la segunda derivada.
EJEMPLO 1

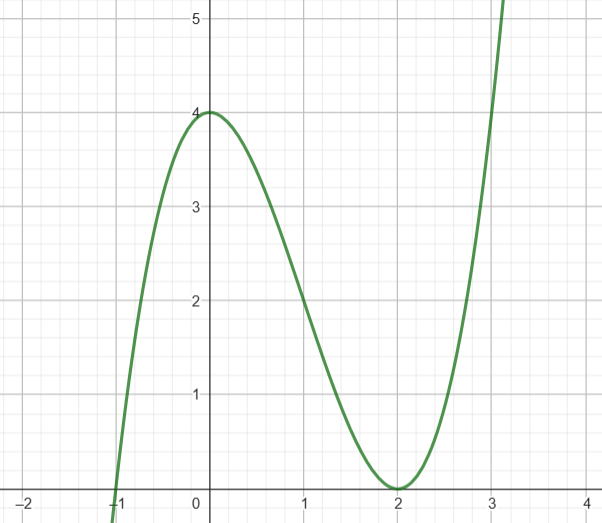



EJEMPLO 2